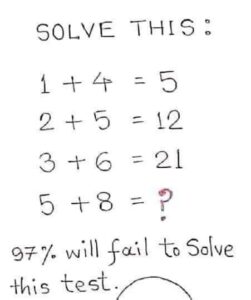
Math problem leaves the internet scratching their heads

It’s to that end that we decided to put the minds of our beloved readers to the test, with a bran-teasing issue that’s left plenty of people across the internet scratching their heads.

So, got your thinking cap on? Ready for this week’s exercise in mathematical gymnastics? I certainly hope so… because here it comes:

If 1+4=5, 2+5=12, and , then what is the value of 5+8?

Perhaps it’s easier if you see it written out as follows:

1+4=5
2+5=12
3+6=21
5+8=?

It appears that this particular problem has left a large portion of the internet scratching their heads, and a lot of people split on what the correct answer actually is. Much of it depends on how you approach the exercise of course; what exact method you employ to try and help you find the right answer.

And the crux of it all? There’s more than one correct answer! In fact, there are quite a few if our research is anything to go by. If you’ve had a go at the problem yourself and want to see if you’ve got it right (or if, like me, you were ultimately left so frustrated that you simply have to be given the answer) see below for five different ways the problem can be tackled.

Solution one

1 + 4 = 5
2 + 5 = 2 + 2(5) = 12
3 + 6 = 3 + 3(6) = 21
5 + 8 = 5 + 5(8) = 45
ALGORITHM: A + A(B) = C
ANSWER = 45

Solution two

1 + 4 = 1 + 4 + (0) = 5
2 + 5 = 2 + 5 + (5) = 12
3 + 6 = 3 + 6 + (12) = 21
5 + 8 = 5 + 8 + (21) = 34
ALGORITHM: A + B + C’ = C, where C’ is the previous answer
ANSWER = 34

Solution Three

1 + 4 = 5 = 5
2 + 5 = (5 + 2) + (5) = 12
3 + 6 = (7 + 2) + (12) = 21
5 + 8 = (9 + 2) + (21) = 32
ALGORITHM: for {X=5, C = X + C’ , X = X+2 };, where C’ is the previous answer. A and B not used in equation,
ANSWER = 32

Solution Four

1 + 4 = 5
2 + 5 = 7 (base 5) =12
3 + 6 = 9 (base 4) = 21
5 + 8 = 13 (base 3) = 111
ALGORITHM: for {X=6, C = (A + B)^(10 -> X), X -1} (First answer in Base6, then Base 5, then 4, etc…)
ANSWER = 111

Solution Five

1 + 4 = 5
2 + 5 = 7 (base 5) =12
3 + 6 = 9 (base 4) = 21
4 + 7 = 11 (base 3) = 102
5 + 8 = 13 (base 2) (aka binary) = 1101
ALGORITHM: for {X=6, C = (A + B)^(10 -> X), X -1} (First answer in Base6, then
Base 5, then 4, etc…including “missing” numbers
ANSWER = 1101